
Zadanie Tramwaj (tra)
Pomóż nam usprawnić bazę zadań!
Tramwaj
Limit pamięci: 64 MB
Bajtazar wyjrzał przez okno i zobaczył zabytkowy model tramwaju na przystanku przed swoim domem. Chciał zrobić mu zdjęcie do swojej kolekcji zdjęć starych pojazdów, jednak zanim znalazł aparat, tramwaj już odjechał.
Bajtazar mieszka w Bajtogrodzie.
W mieście jest  skrzyżowań ponumerowanych od
skrzyżowań ponumerowanych od 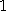 do
do  i przy każdym skrzyżowaniu znajduje się przystanek tramwajowy.
Komunikacja miejska jest tam wyjątkowo punktualna i tramwaje przyjeżdżają na przystanki dokładnie o pełnych minutach.
Bajtazar postanowił więc, że będzie wyglądał przez okno co minutę, mając nadzieję, że unikatowy tramwaj znów pojawi się na przystanku.
Po kilku chwilach stało się to męczące, dlatego Bajtazar potrzebował mądrzejszego rozwiązania.
Wziął mapę Bajtogrodu, zamyślił się głęboko (nie było to łatwe, bo co minutę wyglądał przez okno)
i ustawił aparat tak, by robił zdjęcia przystanku co
i przy każdym skrzyżowaniu znajduje się przystanek tramwajowy.
Komunikacja miejska jest tam wyjątkowo punktualna i tramwaje przyjeżdżają na przystanki dokładnie o pełnych minutach.
Bajtazar postanowił więc, że będzie wyglądał przez okno co minutę, mając nadzieję, że unikatowy tramwaj znów pojawi się na przystanku.
Po kilku chwilach stało się to męczące, dlatego Bajtazar potrzebował mądrzejszego rozwiązania.
Wziął mapę Bajtogrodu, zamyślił się głęboko (nie było to łatwe, bo co minutę wyglądał przez okno)
i ustawił aparat tak, by robił zdjęcia przystanku co 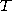 minut.
Liczbę
minut.
Liczbę 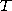 dobrał tak, by była największą taką liczbą całkowitą, że jeśli aparat robi zdjęcia przystanku
co
dobrał tak, by była największą taką liczbą całkowitą, że jeśli aparat robi zdjęcia przystanku
co 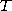 minut od pierwszego przyjazdu zabytkowego tramwaju, to niezależnie od trasy, jaką ten tramwaj
pojedzie, każde jego następne pojawienie się przed domem Bajtazara zostanie uwiecznione na zdjęciu.
minut od pierwszego przyjazdu zabytkowego tramwaju, to niezależnie od trasy, jaką ten tramwaj
pojedzie, każde jego następne pojawienie się przed domem Bajtazara zostanie uwiecznione na zdjęciu.
Bajtazara bardzo zaciekawił uzyskany wynik i zaczął się zastanawiać, jaki rezultat (oznaczmy go przez 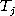 )
otrzymałby, gdyby mieszkał przy innym,
)
otrzymałby, gdyby mieszkał przy innym, 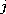 -tym przystanku.
-tym przystanku.
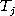 to zatem największa taka liczba całkowita, że jeśli Bajtazar mieszka przy skrzyżowaniu
to zatem największa taka liczba całkowita, że jeśli Bajtazar mieszka przy skrzyżowaniu 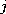 , a tramwaj pojawił się
na przystanku w minucie 0, to wszystkie następne pojawienia się tramwaju, niezależnie od tego,
po jakiej trasie się on porusza, wystąpią w minutach będących całkowitymi wielokrotnościami
, a tramwaj pojawił się
na przystanku w minucie 0, to wszystkie następne pojawienia się tramwaju, niezależnie od tego,
po jakiej trasie się on porusza, wystąpią w minutach będących całkowitymi wielokrotnościami 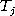 .
Jeśli z
.
Jeśli z 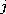 -tego skrzyżowania nie wychodzą żadne tory, lub tramwaj, który
wyjedzie z tego skrzyżowania, na pewno w to miejsce nie powróci, to
-tego skrzyżowania nie wychodzą żadne tory, lub tramwaj, który
wyjedzie z tego skrzyżowania, na pewno w to miejsce nie powróci, to 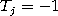 .
.
Wejście
W pierwszym wierszu standardowego wejścia znajdują się dwie liczby całkowite  i
i 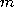 (
(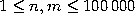 ),
oddzielone pojedynczym odstępem i oznaczające odpowiednio liczbę skrzyżowań w mieście oraz liczbę połączeń między nimi.
Skrzyżowania są ponumerowane od
),
oddzielone pojedynczym odstępem i oznaczające odpowiednio liczbę skrzyżowań w mieście oraz liczbę połączeń między nimi.
Skrzyżowania są ponumerowane od 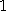 do
do  .
W kolejnych
.
W kolejnych 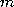 wierszach znajduje się opis sieci tramwajowej w Bajtogrodzie.
W
wierszach znajduje się opis sieci tramwajowej w Bajtogrodzie.
W 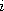 -tym z tych wierszy znajdują się trzy liczby całkowite
-tym z tych wierszy znajdują się trzy liczby całkowite 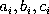 (
(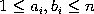 ,
, 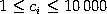 ),
pooddzielane pojedynczymi odstępami i oznaczające, że tramwaj może przejechać ze skrzyżowania
),
pooddzielane pojedynczymi odstępami i oznaczające, że tramwaj może przejechać ze skrzyżowania 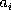 do
do 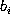 w ciągu
w ciągu 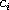 minut.
Wszystkie odcinki torów są jednokierunkowe, jednak może się zdarzyć, że istnieją zarówno tory od skrzyżowania
minut.
Wszystkie odcinki torów są jednokierunkowe, jednak może się zdarzyć, że istnieją zarówno tory od skrzyżowania
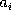 do
do 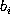 , jak i z
, jak i z 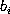 do
do 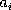 .
Może się również zdarzyć, że
.
Może się również zdarzyć, że 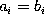 (pętla tramwajowa).
Pomiędzy parą skrzyżowań istnieje co najwyżej jedno połączenie w danym kierunku.
(pętla tramwajowa).
Pomiędzy parą skrzyżowań istnieje co najwyżej jedno połączenie w danym kierunku.
Zakładamy, że czasy postoju tramwaju na przystankach są pomijalne oraz że tramwaj jeździ tak długo, aż trafi w ślepy zaułek lub nieskończenie długo, jeżeli to nigdy nie nastąpi.
Wyjście
Na standardowe wyjście należy wypisać  liczb całkowitych w osobnych wierszach.
W
liczb całkowitych w osobnych wierszach.
W 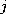 -tym wierszu należy wypisać wartość
-tym wierszu należy wypisać wartość 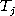 .
.
Przykład
Dla danych wejściowych:
7 8 1 2 1 2 3 4 3 2 4 4 6 3 6 5 3 3 3 2 5 4 4 5 7 1
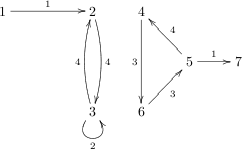
poprawną odpowiedzią jest:
-1 2 2 10 10 10 -1
Wyjaśnienie do przykładu: Tramwaj, który wyjedzie ze skrzyżowania numer 2, może powrócić na przykład po 8, 10 albo 12 minutach. Zatem aby aparat nie przegapił żadnego powrotu tramwaju na przystanek, musi robić zdjęcie co dwie minuty.
Autor zadania: Jakub Łącki.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English